Introduction
This is a series of blog posts related to alternatives to Reinforcement Learning by Human Feedback, created as a joint effort between Argilla and MantisNLP teams. Please ensure you have gone through the previous entries in the series to fully understand the context and progression of the discussion before moving on to this segment. Scroll to the bottom of the page to go to the next blog post of the series.
In previous posts, we started by analyzing the efforts to carry out Supervised Fine-tuning (SFT) and Reinforcement Learning with Human Feedback (RLHF), and the importance of having high-quality data (first and second blog posts). Nevertheless, RLHF is complex and usually unstable, so we examined a promising alternative, Direct Preference Optimization (DPO), to align the LLM with human preferences without requiring RL (third blog post). Still, DPO does not solve all the shortcomings, for instance, a large amount of preference data is needed to fine-tune. To tackle this, researchers have come up with new methods. Some of them are Reinforcement Learning AI Feedback (RLAIF) or Self-Play Fine-Tuning (SPIN) (fourth and fifth blog posts).
In this case, we'll examine Identity Preference Optimization (IPO) which aims to enhance data alignment and mitigate overfitting.
Identity Preference Optimization (IPO)
Seeking simpler and more efficient algorithms to better align LLMs to data, the DeepMind team introduced “A General Theoretical Paradigm to Understand Learning from Human Preferences” with a new general objective and a new algorithm that will be explained along this post.
If you're looking to dive into a practical aspect, the IPO feature is already integrated into the DPO trainer within the TRL library by Hugging Face. However, there's a small catch: due to a discrepancy, you must use the main branch of TRL to access this feature.
Every research starts somewhere, so what sparked the curiosity that led to this one? In light of RLHF's issues, researchers aimed to address the challenges associated with the most common approaches to RLHF, providing new insights.
On one side, they noted that there is the assumption that pointwise rewards can replace pairwise preferences. When using these methods, the Bradley-Terry model is applied to convert the pairs to Elo scores (or logit preferences). Essentially, this model determines each item's relative strength by analyzing pairwise comparisons. In this scenario, where A is preferred over B, and B over C (A > B and B > C), the model will assign individual scores to A, B, and C. To do so, it calculates the likelihood of each pair being chosen in the observed manner (e.g. the likelihood that A is preferred over B) and maximizes it to adjust the strength values (scores) so that they reflect all the observed comparisons (A > B and B > C). This way, we would get unique scores for each item e.g., A=0.6, B=0.3, and C=0.1. Those would be the pointwise scores.
As we can see, the approach is based on two key principles: transitivity, which means if A is preferred over B, and B is preferred over C, then A should be preferred over C; and additivity, where the difference in scores represents the strength of preference. However, this maximization can lead to non-logical or unexpected decisions that do not perfectly match real-world choices. One person may prefer A while another may prefer C, highlighting the gap between mathematical models and human behavior.
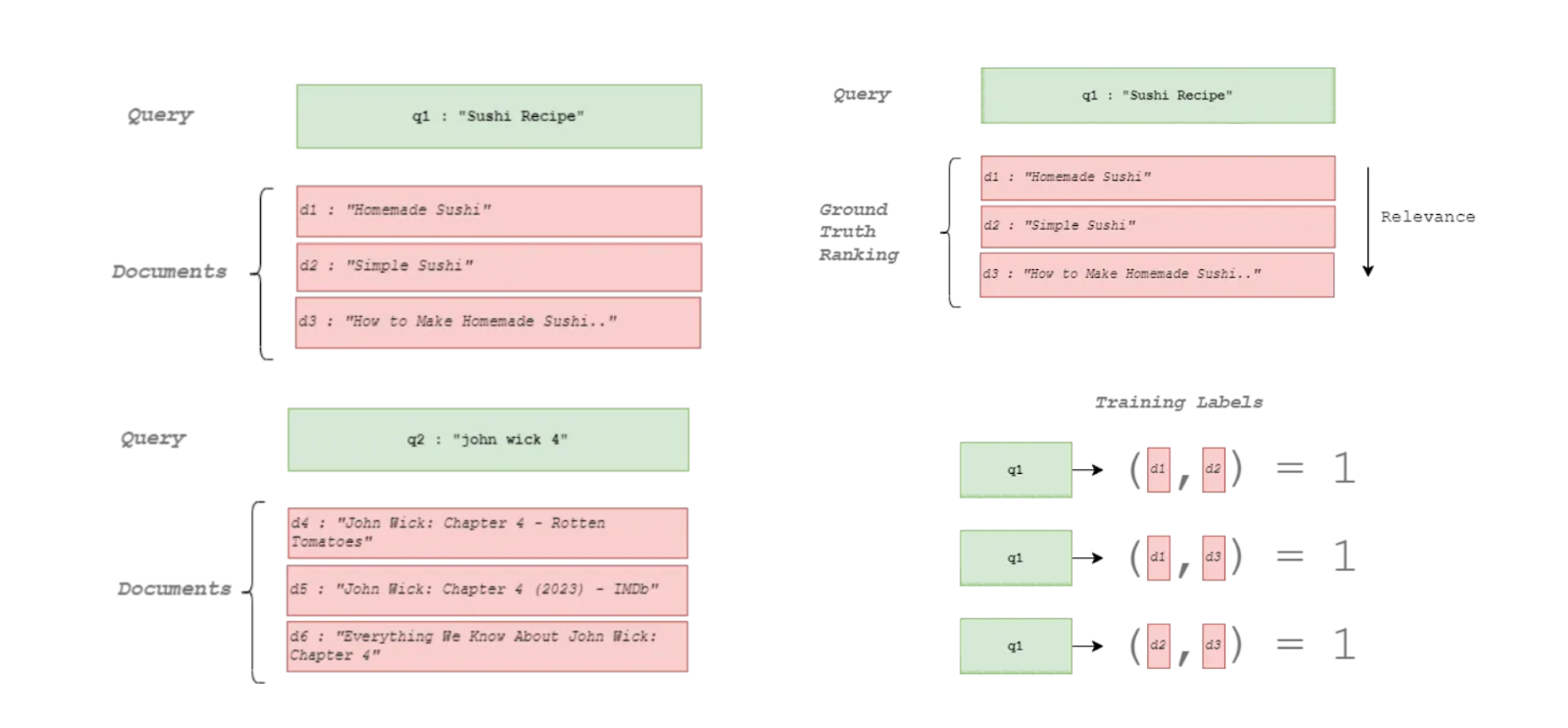On the left, there is a pointwise example, where each document, when paired with the query, is treated as an independent instance. On the right, there is a pairwise example, where the documents are compared in pairs to decide the order. Source: https://towardsdatascience.com/what-is-learning-to-rank-a-beginners-guide-to-learning-to-rank-methods-23bbb99ef38c
Conversely, a reward model is often trained on these pointwise rewards, allowing generalization. And although DPO gets rid of this reward model by targeting the logit-transformed versions of the actual preferences during the optimization, still perpetuates the previous idea. So, the main issue arises because the pointwise reward system disproportionately rewards small increases in preference probabilities, leading to problems of overfitting and weak regularization. This complicates the model's ability to generalize and accurately reflect true preferences. We’ll delve deeper into this problem later in this post.
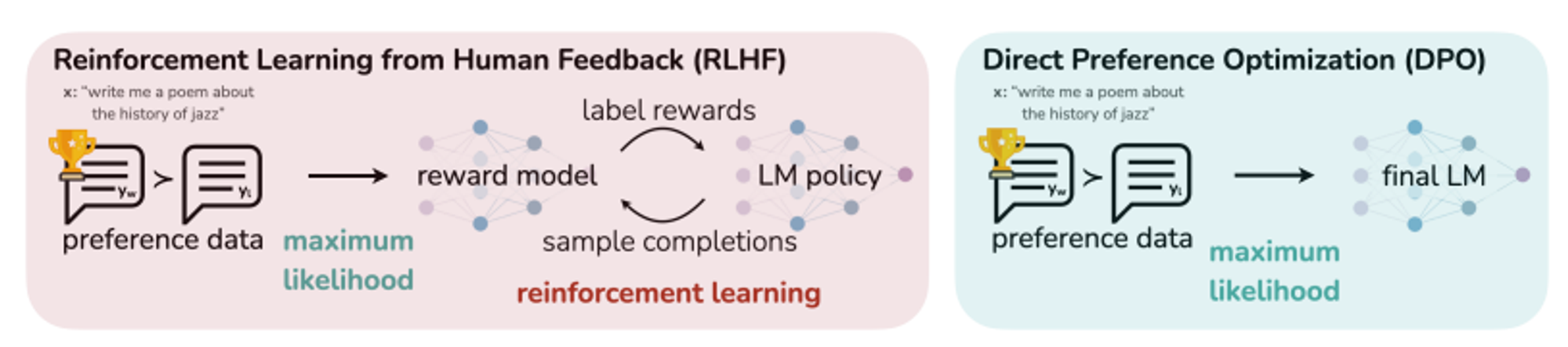Example of preference optimization in RLHF and DPO. Remember that DPO does not use an explicit reward model. Source: https://arxiv.org/pdf/2305.18290.pdf
To better understand how these approaches work and how to overcome their weaknesses, they introduced two new ideas: ΨPO and IPO. The main innovation here is eliminating the reward model while keeping the pairwise comparison aspect, aiming to solve the model's limitations by adjusting the training process.
The key points: ΨPO and IPO
On one hand, the researchers identified that the RLHF and DPO objectives could be unified into a more general objective, ΨPO, which offered a broader theoretical basis for preference learning. Through their analysis of ΨPO, they pinpointed issues like weak regularization and the potential for overfitting.
Typically, RLHF and DPO use KL-regularization to ensure that the LLM improves incrementally with each training step, avoiding significant deviations from the original, non-aligned model. Nevertheless, they noticed a problem: as the model's predictions become more deterministic (that is, predictable), this form of regularization becomes less effective. Ideally, regularization should distinguish between small and large increases, so that it encourages the model to focus on making significant improvements where there is greater uncertainty rather than excessively fine-tuning where the model is already confident. However, in the current scenario, the regularization doesn't sufficiently make this difference, leading to a less nuanced learning process.
Let's say it's like a tutor teaching a child to read. In the beginning, the teacher will make small corrections (KL regularization) to ensure that the student improves without developing bad habits. However, as his skill improves and his reading becomes more deterministic if the guidance is the same, it's like giving the same level of correction whether the child gets confused between “cat” and “cap” or mixes up “butterfly” with “ball”.
On the other hand, unlike traditional methods that may use tricks like early stopping for regularization, they introduced a special case of ΨPO: Identity-PO. IPO optimizes the preferences even without relying on a reward model and, in scenarios, where preferences are deterministic, ensuring the effectivity of the KL-regularization.
By replacing the logit function with the identity function, IPO optimizes preferences directly (learning from pairwise preferences instead of the logit preferences). It compares the preferred actions over non-preferred ones with a reference policy, incorporating a term to manage the regularization effectively. This regularization mechanism allows IPO to strike a balance between adapting to training data and maintaining generalization capabilities, which is essential for the model's performance on unseen data.
Following the previous example, if the child initially prefers reading simple over complex words, by using the identity function the rewards will be proportional and direct (they will get stickers instead of a numeric score). The guideline (reference policy) will indicate this preference, but the regularization term will reward him for reading simple words and also encourage him to tackle complex words occasionally.
For a more theoretical approach and mathematical proof, check the original paper.
IPO vs DPO
To prove the efficiency of IPO, they also compared it to DPO with different tau (τ) values for the KL-regularization. The τ parameter helps to adjust the strength of the regularization term: a higher τ value encourages more exploration by the model, while a lower τ value promotes more exploitation of the learned preferences.
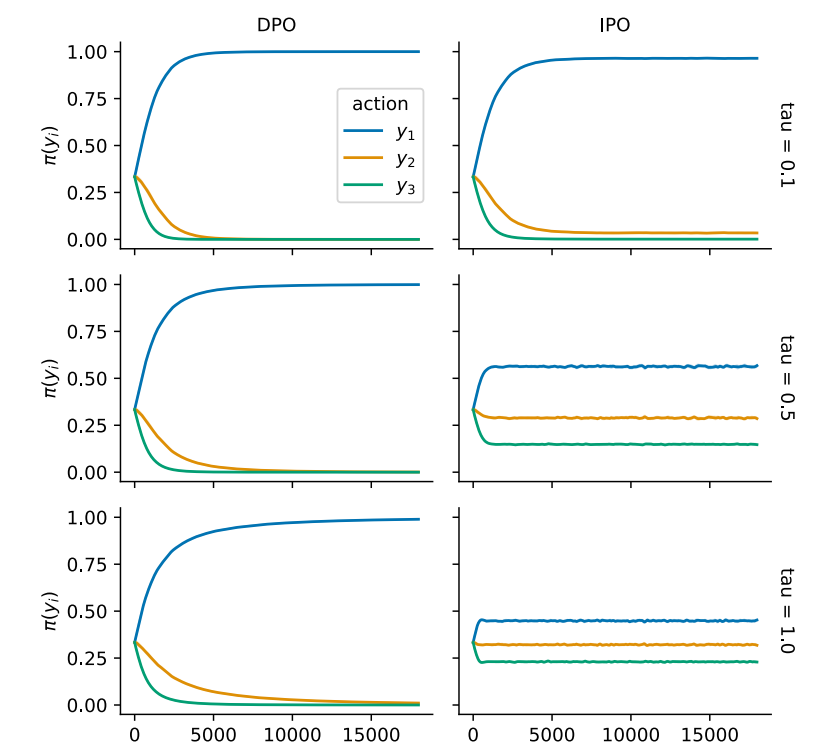Comparison between the learning curves of action probabilities of IPO and DPO for D1 = (A, B), (B, C), (A, C), which represent a total ordering. Source: https://arxiv.org/pdf/2310.12036.pdf.
Given an example dataset, where 1 is preferred over 2 and 3, the above image shows the learning curves for DPO and IPO. In both cases, the preference order is correctly determined. However, we can observe that with different regularization parameters, DPO remains unchanged, which verifies one of this paper’s hypotheses. Moreover, DPO shows overfitting as their curves always converge for 2 and 3, while the preferred value of 1 nearly gets to a probability of 1. In contrast, there is a clear difference in the curves of IPO when applying the different τ values and how the three samples are distinguishable and ranked.
The Hugging Face team also compared DPO, KTO, and IPO across the MT benchmark. Depending on the model, here the results are varied and while with Zephyr the results are benefited by IPO, the same conclusions are not replicated for OpenHermes.
For more information on the experiments performed, check the following post.
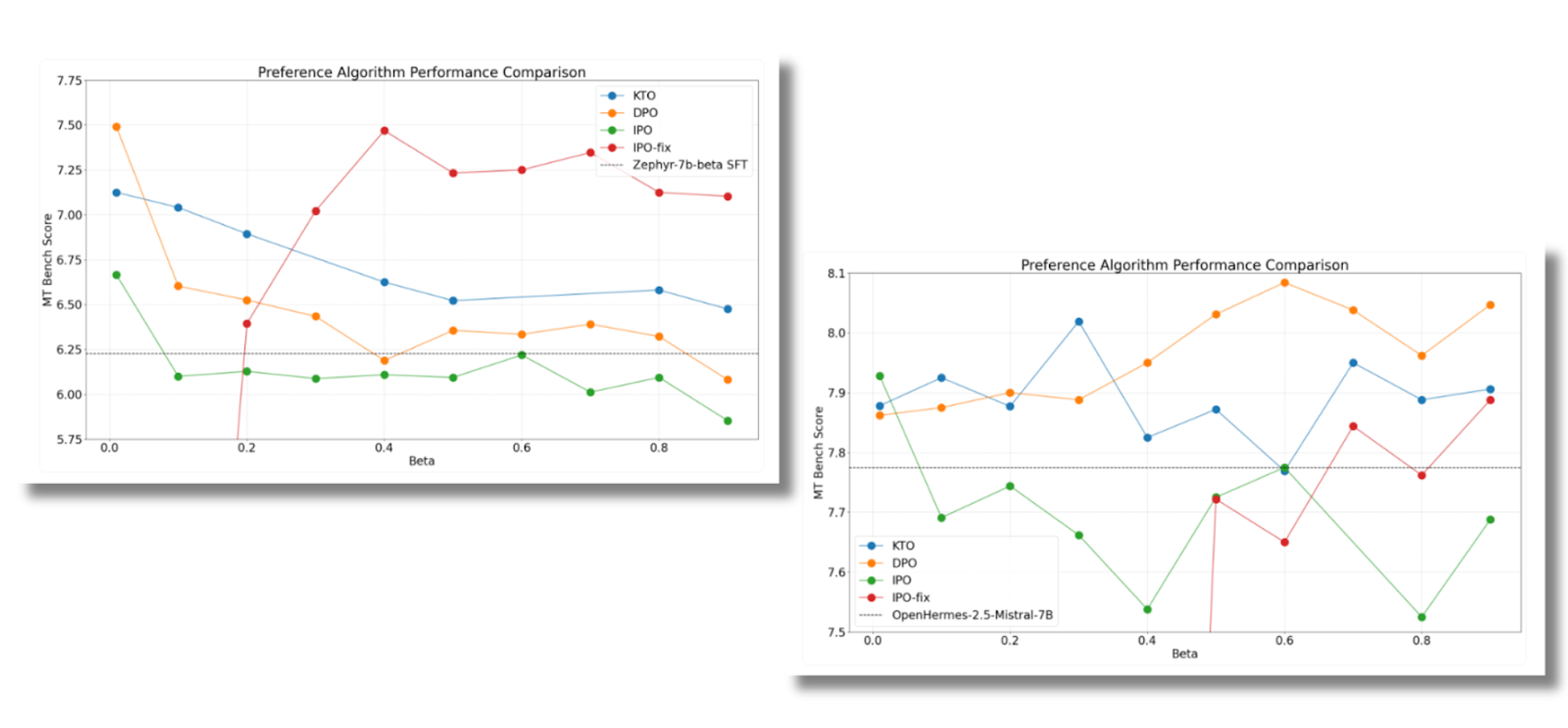MT-Bench scores for the Zephyr model (on the left) and OpenHermes (on the right) for different β (=tau). Source: https://huggingface.co/blog/pref-tuning
The outcomes of implementing IPO are not definitive, indicating that further experiments are necessary. Despite the thorough theoretical analysis supporting IPO's validity, there is a call for more empirical evidence, particularly in complex and real-world scenarios, to strengthen the case for IPO's effectiveness.
It should also be noted that in response to the claims made in favor of IPO, Eric Mitchell, an author of the DPO paper, also published a one-page document. There he advocated for DPO, proposing some modifications to alleviate the problems with regularization and addressing the theoretical concerns in the IPO discussion.
Conclusion
In conclusion, the IPO paper provides a strong theoretical framework explaining the basis of RLHF and DPO through ΨPO and highlighting the major shortcomings of these approaches. Furthermore, to avoid overfitting and weak regularization, a new solution with IPO that adds a regularization term was introduced. Despite criticisms regarding the limited empirical testing and the mixed results, IPO's approach remains noteworthy. It should be considered among the new methodologies in this field, offering a valuable perspective for advancing preference-based learning models.
Want to know more?
This is the sixth entry of a series of blog posts dedicated to alternatives to RLHF. The first, second, third, fourth and fifth posts of the series can be found on our website too.
Argilla and Mantis NLP teams are happy to help with any question you may have about preparation steps for training a LLM using Supervised fine-tuning, Reinforcement Learning, or Direct Preference Optimization.
All the data curation steps are currently supported by Argilla’s Data Platform for LLM, and from Mantis NLP we offer end-to-end support for the whole process.
